15. Categorical Cross-Entropy
Categorical Cross-Entropy
Previously we've been using the sum of squared errors as the cost function in our networks, but in those cases we only have singular (scalar) output values.
When you're using softmax, however, your output is a vector. One vector is the probability values from the output units. You can also express your data labels as a vector using what's called one-hot encoding.
This just means that you have a vector the length of the number of classes, and the label element is marked with a 1 while the other labels are set to 0. In the case of classifying digits from before, our label vector for the image of the number 4 would be:
\mathbf{y} = [0,0,0,0,1,0,0,0,0,0]And our output prediction vector could be something like\mathbf{\hat y} = [ 0.047, 0.048, 0.061, 0.07, 0.330,0.062, 0.001, 0.213, 0.013, 0.150].
We want our error to be proportional to how far apart these vectors are. To calculate this distance, we'll use the cross entropy. Then, our goal when training the network is to make our prediction vectors as close as possible to the label vectors by minimizing the cross entropy. The cross entropy calculation is shown below:
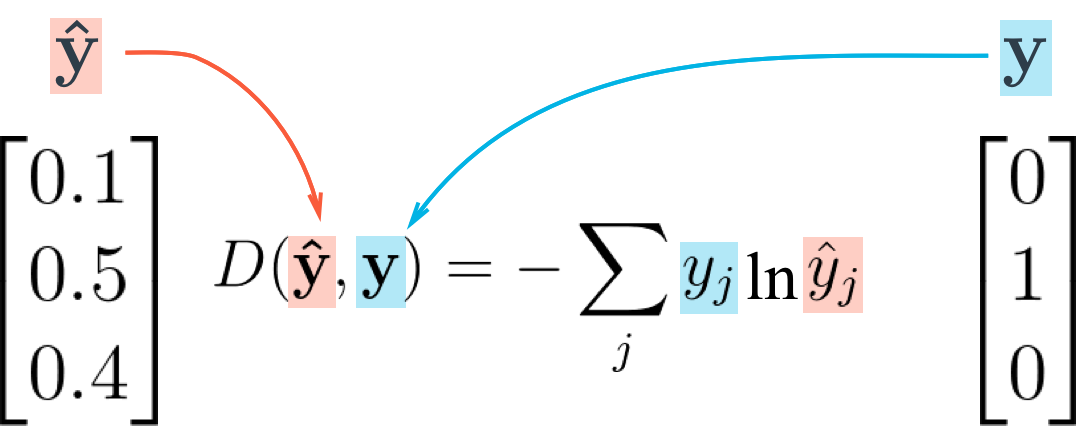
Cross entropy calculation
As you can see above, the cross entropy is the sum of the label elements times the natural log of the prediction probabilities. Note that this formula is not symmetric! Flipping the vectors is a bad idea because the label vector has a lot of zeros and taking the log of zero will cause an error.
What's cool about using one-hot encoding for the label vector is that y_j is 0 except for the one true class. Then, all terms in that sum except for where y_j = 1 are zero and the cross entropy is simply D = - \ln \hat{y} for the true label. For example, if your input image is of the digit 4 and it's labeled 4, then only the output of the unit corresponding to 4 matters in the cross entropy cost.
Cross Entropy